Bất đẳng thức đáng nhớ là một phần quan trọng trong chương trình học toán của học sinh. Biết được thế nào là bất đẳng thức, bất đẳng thức côsin (am-gm), bất đẳng thức bunhiacopxki, bất đẳng thức schwarz … sẽ giúp các em tìm ra lời giải cho bài toán của mình. Cùng 25giay.vn tìm hiểu những bất đẳng thức khó quên trong bài viết dưới đây nhé!
Lý thuyết bất đẳng thức? Bất đẳng thức đáng nhớ Bất đẳng thức cosi (hoặc bất đẳng thức am-gm) Bất đẳng thức bunhiacopxki là gì?
Lý thuyết Bất bình đẳng? Bất đẳng thức đáng nhớ
Định nghĩa của bất đẳng thức là gì?
Trong toán học, bất đẳng thức là một phát biểu về mối quan hệ thứ tự giữa hai đối tượng, là biểu thức chứa số và phép toán.
Xem: Bất bình đẳng am-gm là gì
Biểu thức ở vế trái của dấu bất đẳng thức được gọi là vế trái, và biểu thức ở vế phải được gọi là vế phải của dấu bất đẳng thức.
Định nghĩa của bất bình đẳng tuyệt đối là gì?
Khi một bất đẳng thức tuân theo tất cả các giá trị của tất cả các biến có trong bất đẳng thức, nó được gọi là bất đẳng thức tuyệt đối hoặc bất đẳng thức không điều kiện.
Một bất đẳng thức được gọi là bất đẳng thức có điều kiện khi nó đúng với một số giá trị của một biến và ngược lại hoặc không còn đúng với các giá trị khác. Một bất đẳng thức đúng vẫn đúng nếu nó cộng hoặc trừ cùng một giá trị trên cả hai vế, hoặc nhân hoặc chia cả hai vế cho cùng một số dương.
Nếu cả hai vế của một bất đẳng thức được nhân hoặc chia cho một số âm, thì bất đẳng thức sẽ bị đảo ngược. Đây là những điều cơ bản, nhưng quan trọng đối với bất đẳng thức đáng nhớ.
Định nghĩa 1: Mối quan hệ hoàn toàn không bình đẳng
Người ta nói rằng số thực a lớn hơn số thực b và nó được ghi là a> b Khi a-b là một số dương, nghĩa là (a-b> 0), hoặc nó cũng được ghi là b
Chúng ta có: (a> bleftrightarrow a-b> 0)
Nếu a & gt; case b hoặc a = b, nó có thể được biểu thị bằng (ageq b).
Chúng tôi có: (ageq bleftrightarrow a-bgeq0)
Định nghĩa 2
Giả sử a và b là hai biểu thức (biểu thức có thể là số hoặc chứa biến)
Chúng ta có một mệnh đề: “a lớn hơn b”, được ký hiệu là (a> b)
“a nhỏ hơn b”, ký hiệu (a
“a nhỏ hơn hoặc bằng b”, ký hiệu (a leq b)
“a lớn hơn hoặc bằng b”, ký hiệu (a geq b)
Nó được gọi là bất đẳng thức.
Quy ước: – Khi chúng ta nói về bất bình đẳng và không nói gì khác, chúng ta hiểu rằng đó là một bất bình đẳng thực sự.
Chứng minh một bất đẳng thức sẽ chứng minh rằng bất đẳng thức là đúng.
Các loại câu hỏi phổ biến nhất về chủ đề bất bình đẳng là:
Chứng minh bất đẳng thức. Giải bất phương trình (tìm tập giá trị của một biến làm cho bất đẳng thức đúng). Các bài toán cực trị (tìm giá trị lớn nhất và nhỏ nhất của một biểu thức để xác định một hoặc nhiều biến.
Các bất đẳng thức cơ bản cho các số thực dương và âm
Trong đó a là một số thực dương, chúng tôi ký hiệu là & gt; 0
Trong đó a là số thực âm, chúng tôi ký hiệu là
a là một số thực dương hoặc a = 0, chúng ta nói a là một số thực không âm và có giá trị trung bình (ageq 0)
a là một số thực âm hoặc a = 0, chúng ta nói a là một số thực không dương và có giá trị trung bình (aleq 0)
Đối với hai số thực a và b, chỉ có thể có một trong ba khả năng sau:
A & gt; B, A
Phủ định của mệnh đề “(a> 0)” là mệnh đề “(aleq 0)”
Mệnh đề phủ định “(a
.)
Các tính chất cơ bản của bất đẳng thức
Thuộc tính 1: Thuộc tính cầu nối
Với tất cả các số thực a, b, c, ta có: (left {begin {matrix} a & amp; & gt; & amp; b b & amp; & gt; & amp; c end {matrix} right.rightarrow a & gt; c)
p>
Thuộc tính 2: Các thuộc tính liên quan đến phép cộng và phép trừ trên cả hai vế của một số
Thuộc tính này được biểu thị như sau: phép cộng và phép trừ các số thực giống nhau duy trì mối quan hệ thứ tự trên tập các số thực
Quy tắc cộng cho cả hai bên: (a & gt; b left rightarrow a + c & gt; b + c)
Trừ cùng một số cho cả hai bên: (a> b mũi tên phải a-c> b-c)
Hệ quả 1: Chuyển đổi: (a + c> bleftrightarrow a> b-c)
Thuộc tính 3: Quy tắc cộng hai bất phương trình cùng phương
(left {begin {matrix} a & amp; & gt; & amp; b c & amp; & gt; & amp; d end {matrix} right.rightarrow a + c & gt; b + d)
Thuộc tính 4: Các thuộc tính liên quan đến phép nhân và chia cả hai vế của một bất đẳng thức
Thuộc tính được biểu thị như sau:
Phép nhân (hoặc phép chia) với các số thực dương bảo toàn mối quan hệ thứ tự trên tập hợp các số thực và phép nhân (hoặc phép chia) với các số thực âm đảo ngược mối quan hệ thứ tự trên tập hợp các số thực.
Quy tắc nhân cả hai vế với cùng một số: (a & gt; b left rightarrow sang trái {begin {matrix} ac & amp; & gt; & amp; bc (c & gt; 0) ac & amp;
Quy tắc chia cả hai vế cho cùng một số: (a & gt; b leftrightarrow left {begin {matrix} frac {a} {c} & amp; & gt; & amp; frac {b} {c} (c & gt; 0) phân số {a} {c} & amp;
Hệ quả 2: Các quy tắc thay đổi ký hiệu: (a> bleftrightarrow -a
Thuộc tính 5: Quy tắc nhân cả hai vế của bất đẳng thức: (left {begin {matrix} a & amp; & gt; & amp; b & amp; & gt; & amp; 0 c & amp; & gt; & amp; d & amp; & gt; & amp; 0 end {matrix} right.rightarrow ac & gt; bd) thuộc tính 6: nghịch đảo cả hai vế: (a & gt; b & gt; 0 leftrightarrow 0 property 7: rule for power of n: (a & gt; b & gt; 0, nin n * rightarrow a ^ {n}> b ^ {n}) thuộc tính 8: quy tắc căn bậc n: (a> b> 0, nin n * rightarrow sqrt {a}> sqrt {b})
Kết quả: Quy tắc hình vuông trên cả hai mặt
Nếu a và b là các số dương thì: (a> bleftrightarrow a ^ {2}> b ^ {2})
Nếu a và b là hai số không âm thì: (ageq bleftrightarrow a ^ {2} geq b ^ {2})
Bất bình đẳng giá trị tuyệt đối
Các tính chất của bất đẳng thức đáng nhớ này được tóm tắt như sau:
(left | right | geq 0, left | right | ^ {2} = a ^ {2}, a
Với tất cả a, b trong r, chúng ta có:
(left | a + b right | leq left | a right | + left | b right |) (left | a-b right | leq left | a right | + left | b right |) (left | a + b right | = left | a right | + left | b right | leftrightarrow abgeq 0) (left | a-b right | = left | a right | + left | b right | leftrightarrowableq 0)
Bất đẳng thức của một tam giác là gì?
Nếu a, b, c là ba cạnh của tam giác thì ta có:
(a & gt; 0, b & gt; 0, c & gt; 0) (left | b-c right | (left | c-a right | (left | a-b right | (a & gt; b & gt; c rightarrow a & gt; b & gt; c))
p>
Hàm đơn điệu và bất đẳng thức
Từ định nghĩa của một hàm đơn điệu (tăng hoặc giảm), chúng ta có thể chuyển cả hai vế của bất đẳng thức thành các biến tăng nghiêm ngặt của hàm đơn điệu và kết quả của bất đẳng thức vẫn được giữ nguyên. Ngược lại, nếu chúng ta bao gồm cả hai vế của bất đẳng thức hàm đơn điệu giảm nghiêm ngặt, chúng ta phải đảo ngược bất đẳng thức ban đầu để bất đẳng thức giữ nguyên.
Xem thêm: Crate Recreation – Harsh Dawn Mastery Course Guide
có nghĩa là:
Nếu tồn tại bất đẳng thức không hạn chế (a leq b) (hoặc (a geq b)), thì có hai trường hợp: khi f (x) là một hàm tăng đơn điệu, thì (f (a) leq f (b) ))) (hoặc (f (a) geq f (b)) (không nghịch đảo). Khi f (x) là một hàm giảm đơn điệu, thì (f (a) geq f (b)) (hoặc (f (a) ))) leq f (b)) (đảo ngược). Nếu tồn tại bất đẳng thức a b), cũng có hai trường hợp xảy ra: khi f (x) là một hàm đơn điệu tăng nghiêm ngặt thì (f (a) f (b) )) (Không nghịch đảo. Khi f (x) là một hàm đơn điệu giảm nghiêm ngặt, thì (f (a)> f (b)) (hoặc (f (a)
Bất đẳng thức kép là gì?
Biểu tượng (a
Dễ dàng nhận thấy rằng sử dụng các thuộc tính tương tự như trên, cùng một số có thể được cộng / trừ cho ba số hạng này hoặc cả ba số hạng có thể được nhân / chia cho cùng một số khác 0 và tùy thuộc vào dấu hiệu của số. Nhân / chia mà không đảo ngược bất đẳng thức.
*** Lưu ý: Chỉ thực hiện các thao tác trên với cùng một số, tức là (a
Nói chung, bất đẳng thức kép có thể được sử dụng với bất kỳ số hạng nào: ví dụ: (a_ {1} leq a_ {2} leq… leq a_ {n}) nghĩa là (a_ {i)} leq a_ {i + 1}) trong đó i = 1, 2, 3,,…, n-1. Tương đương với (a_ {i} leq a_ {j} forall 1 leq ileq j leq n)
Đôi khi, ký hiệu bất đẳng thức kép được sử dụng với các bất đẳng thức theo hướng ngược nhau, trong trường hợp đó, ký hiệu này được hiểu là sự ghép các bất đẳng thức khác nhau của hai số hạng liền kề. Ví dụ: (ac leq d) có nghĩa là c và (cleq d)
Trong toán học, ký hiệu này thường được sử dụng, nhưng trong các ngôn ngữ lập trình, chỉ một số ngôn ngữ như python mới cho phép ký hiệu này.
Khi đối mặt với các đại lượng mà các công thức chính xác không thể hoặc không dễ dàng tìm thấy, các nhà toán học thường sử dụng các bất đẳng thức để giới hạn phạm vi giá trị mà các đại lượng này có thể có. .
bất đẳng thức cosic (hoặc bất đẳng thức am-gm)
Bất đẳng thức cosi là gì? Định nghĩa phương trình cosic trong toán học
Bất đẳng thức cosi hoặc bất đẳng thức am-gm thực sự là một bất đẳng thức đáng nhớ cho thấy mối quan hệ giữa giá trị trung bình và giá trị trung bình nhân. Đây là một trong những bất đẳng thức đáng nhớ dùng để chứng minh bất đẳng thức trong các lớp toán THPT.
bất đẳng thức am-gm là tên chính xác của bất đẳng thức cho phương tiện và phương tiện nhân. Có nhiều cách để chứng minh bất đẳng thức này, nhưng cách tốt nhất là chứng minh cosi theo quy nạp (cauchy). Do đó, nhiều người lầm tưởng rằng Cauchy đã phát hiện ra bất đẳng thức này. Theo tên gọi chung quốc tế, bất đẳng thức cosi được gọi là bất đẳng thức am-gm (trung bình số học – trung bình hình học).
Trong toán học, bất đẳng thức cosi là bất đẳng thức so sánh trung bình cộng và trung bình nhân của n số thực không âm, được biểu thị như sau:
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng và trung bình cộng bằng trung bình cộng chỉ khi và chỉ khi n số bằng nhau.
Đối với trường hợp 2 số thực không âm và 3 số thực không âm: thường có n số thực không âm: (x_ {1,}, x_ {2}, x_ {3},… x_ {n}), Chúng tôi có:
(frac {x_ {1} + x_ {2} +… + x_ {n}} {n} geq sqrt {x_ {1} x_ {2}… x_ {n}})
“=” xuất hiện khi và chỉ khi (x_ {1} = x_ {2} =… = x_ {n})
Áp dụng Bất đẳng thức Cosin để Giải quyết Vấn đề
Chứng minh bất đẳng thức cosi cho n số thực không âm

Bất đẳng thức Bunhiacopxki là gì?
Bất đẳng thức bunhiacopxki, chính xác được gọi là bất đẳng thức cauchy – bunhiacopxki – schwarz, do ba nhà toán học độc lập phát hiện và đề xuất và có nhiều ứng dụng trong toán học. Thường được đặt theo tên của nhà toán học Nga bunhiacopxki. Dưới đây là những điều bạn cần biết về bất đẳng thức đáng nhớ này:
Bất đẳng thức bunhiacopxki cơ bản
Đối với hai dãy số thực (a_ {1}, a _ {} 2,… a_ {n}) và (b_ {1}, b _ {} 2,… b_ {n}), chúng ta có:
((a_ {1} b_ {1} + a_ {2} b_ {2} +… + a_ {n} b_ {n}) ^ {2} leq (a_ {1} ^ {2} + a_ {2} ^ {2}… + a_ {n} ^ {2}) (b_ {1} ^ {2} + b_ {2} ^ {2}… + b_ {n} ^ {2}))
Nếu và chỉ khi (frac {a_ {1}} {b_ {1}} = frac {a_ {2}} {b_ {2}} =… = frac {a_ {n}} {b_ {n} })
bất đẳng thức bunhiacopxki ở dạng phân số
Đối với hai dãy số thực (a_ {1}, a _ {} 2,… a_ {n}) và (b_ {1}, b _ {} 2,… b_ {n}), chúng ta có:
(frac {a_ {1} ^ {2}} {b_ {2}} + frac {a_ {2} ^ {2}} {b_ {2}} +… + frac {a_ {n} ^ { 2}} {b_ {n}} geq frac {a_ {1} + a_ {2} +… + a_ {n}} ^ {2} {b_ {1} + b_ {2} +… + b_ {n} })
Nếu và chỉ khi (frac {a_ {1}} {b_ {1}} = frac {a_ {2}} {b_ {2}} =… = frac {a_ {n}} {b_ {n} })
Áp dụng công thức bunhiacopxki để giải toán
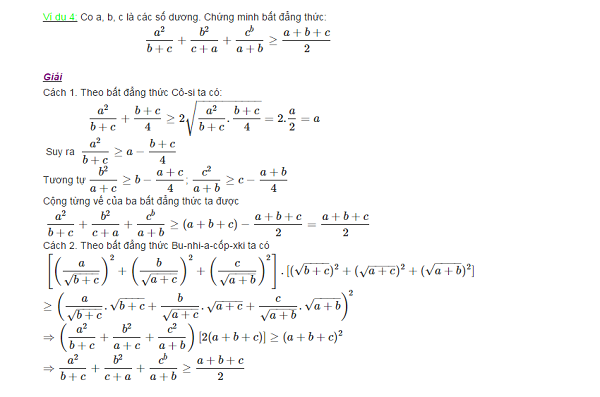
Bất đẳng thức Holder là gì?
Bất đẳng thức giá trị
(được đặt theo tên nhà toán học người Đức Otto Holder), là một bất đẳng thức đáng nhớ liên quan đến không gian (l ^ {p}), được sử dụng để chứng minh tính tổng quát của bất đẳng thức tam giác trong không gian (l ^ {p})
có m dãy số dương ((a_ {1,1}, a_ {1,2},…, a_ {1, n}), (a_ {2,1}, a_ {2,2},…, a_ {2, n})… (a_ {m, 1}, a_ {m, 2},…, a_ {m, n})) Chúng ta có:
(prod_ {i = 1} ^ {m} left (sum_ {j = 1} ^ {n} a_ {i, j} right) geq left (sum_ {j = 1} ^ {n} sqrt {prod_ {i = 1} ^ {m}} a_ {i, j} đúng) ^ {m})
Đẳng thức xảy ra khi m dãy số tương ứng tỷ lệ với nhau.
Bất đẳng thức Cauchy-Charvaz là kết quả của bất đẳng thức giữ nguyên khi m = 2.
bất đẳng thức minkowski (mincopxki)
Giống như bất đẳng thức chủ, bất đẳng thức minkowski dẫn đến kết luận rằng không gian lp là không gian vectơ pháp tuyến.
Xem Thêm: Và hơn thế nữa – Câu đố tiếng Anh: Cách Sử dụng Từ & amp; # 39thêm & amp; # 39
Bất đẳng thức minkowski là một bất đẳng thức đáng nhớ với công thức cụ thể sau:
Với hai dãy số thực (a_ {1}, a_ {2},…, a_ {n}) và (b_ {1}, b_ {2},…, b_ {n}) chúng ta có:
p>
(sqrt {a_ {1} ^ {2} + b_ {1} ^ {2}} + sqrt {a_ {2} ^ {2} + b_ {2} ^ {2}} +… + sqrt { a_ {n} ^ {2} + b_ {n} ^ {2}} geq sqrt {(a_ {1} + a_ {2} +… + a_ {n}) ^ {2} + {}} (b_ { 1} + b_ {2} +… + b_ {n}) ^ {2})
Bất đẳng thức Minkowski mở rộng:
Với hai dãy số thực (a_ {1}, a_ {2},…, a_ {n}) và (b_ {1}, b_ {2},…, b_ {n}) chúng ta có:
p>
(sqrt {a_ {1} a_ {2}… a_ {n}} + sqrt {b_ {1} b_ {2}… b_ {n}} leq sqrt {(a_ {1} + b_ {1} ) (a_ {2} + b_ {2})… (a_ {n} + b_ {n})})
Dấu “=” của bất đẳng thức Minkowski giống với của Cauchy-Schwartz
Bất đẳng thức Schwartz là gì?
Bất đẳng thức Schawarz còn được gọi là bất đẳng thức cauchy, bất đẳng thức cauchy schwarz, bất đẳng thức cauchy-buyakovski-schwarz. Bất đẳng thức Schwartz, hay bất đẳng thức Cauchy-Buniakovsky-Schwartz, được đặt theo tên của ba nhà toán học nổi tiếng, Augustine Louis Cauchy và Victor Yakovlevich Bunia. Được đặt theo tên của Kowski và Herman Armandus Schwartz.
Đây là một bất đẳng thức đáng nhớ thường được sử dụng trong nhiều lĩnh vực toán học khác nhau, chẳng hạn như vectơ trong đại số tuyến tính, giải tích cho chuỗi vô hạn và tích phân, và phương sai trong lý thuyết xác suất.
Cho hai dãy số thực (a_ {1}, a_ {2},…, a_ {n}) và (b_ {1}, b_ {2},…, b_ {n}) và (b_ { i)} geq 0) Chúng tôi có:
(frac {a_ {1} ^ 2} {b_ {1}} + frac {a_ {2} ^ 2} {b_ {2}} +… + frac {a_ {m} ^ 2} {b_ { m}} geq frac {(a_ {1} + a_ {2} +… + a_ {m}) ^ 2} {b_ {1} + b_ {2} +… + b_ {m}})
Bất đẳng thức Chebyshev là gì?
Bất đẳng thức Chebyshevga cũng là một bất đẳng thức quan trọng và đáng nhớ. Nó được đặt theo tên của nhà toán học Pavnuti Chebyshev:
(bên trái {begin {matrix} a_ {1} & amp; geq & amp; a_ {2} geq & amp; … & amp; geq & amp; a_ {n} b_ {1} & amp; geq & amp; b_ {2 } geq & amp;… & amp; geq & amp; b_ {n} end {matrix} right.)
Suy luận: (frac {1} {n} sum_ {k = 1} ^ {n} a_ {k} b_ {k} geqleft (frac {1} {n} sum_ {k = 1} ^ {n} a_ {k} right) left (frac {1} {n} sum_ {k = 1} ^ {n} b_ {k} right))
(bên trái {begin {matrix} a_ {1} & amp; geq & amp; a_ {2} geq & amp; … & amp; geq & amp; a_ {n} b_ {1} & amp; leq & amp; b_ {2 } leq & amp;… & amp; leq & amp; b_ {n} end {matrix} right.)
=> (frac {1} {n} sum_ {k = 1} ^ {n} a_ {k} b_ {k} leqleft (frac {1} {n} sum_ {k = 1} ^ {n} a_ {k} right)) left (frac {1} {n} sum_ {k = 1} ^ {n} b_ {k} right))
Trên đây là tổng hợp những kiến thức về bất đẳng thức cơ bản và quan trọng nhất. Hy vọng bài viết trên đây của 25giay.vn đã giúp bạn hiểu được bất đẳng thức là gì? Các công thức của bất đẳng thức cosi, bất đẳng thức bunhiacopxki, bất đẳng thức schwarz … Nếu bạn có bất kỳ đóng góp nào cho bài viết về bất đẳng thức đáng nhớ hoặc có bất kỳ câu hỏi nào, hãy để lại bình luận và cho chúng tôi biết. Chúng ta hãy nói chuyện nhiều hơn!
