Công thức diện tích xung quanh
– Các khái niệm
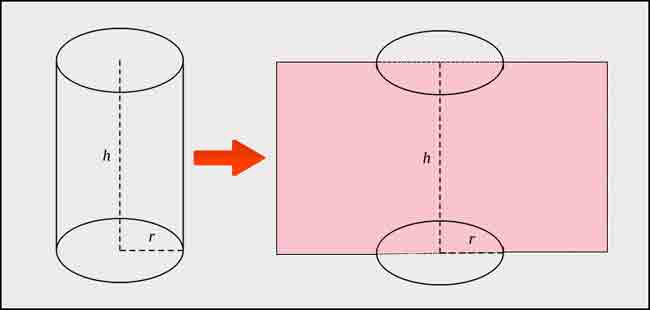
Diện tích xung quanh hình trụ chỉ bao gồm diện tích xung quanh bề mặt xung quanh của hình trụ, không bao gồm hai đáy.
Diện tích hình trụ thường được biểu diễn bằng hai khái niệm: xung quanh và chung.
- Diện tích Hình trụ chỉ bao gồm diện tích của chu vi xung quanh hình trụ, không bao gồm diện tích của hai đáy.
- Tổng diện tích được tính bằng kích thước của toàn bộ không gian hình bị chiếm dụng, bao gồm diện tích chu vi và diện tích của hai đáy hình tròn.
-Formula
Công thức tính diện tích xung quanh bằng chu vi của hình tròn cơ sở nhân với chiều cao.
Bạn đang xem: Công thức về diện tích xung quanh hình trụ
sxq = 2.π.r.h
Ở đâu :
– r: Bán kính của hình trụ.
-h: Chiều cao từ đáy đến đỉnh của hình trụ.
– = 3,14159265359

– Ví dụ
Một hình trụ có bán kính đáy r = 5 cm và chiều cao h = 7 cm. Tính diện tích xung quanh của một hình trụ đứng.
Mô tả lời giải : Diện tích xung quanh của hình trụ: sxq = 2.π.r.h = 2π.5.7 = 70π = 219.8 (cm2).
Ví dụ 1: Một bóng đèn huỳnh quang có chiều dài 1,2m và đường kính hình tròn đế 4cm được đặt trong một ống bìa cứng hình hộp (h.82). Tính diện tích của tấm bìa cứng được dùng để làm hộp.
Giải pháp:
Diện tích của tấm bìa cứng cần tính là diện tích xung quanh một hình hộp có đáy là 4cm và chiều cao là 1,2m = 120cm.
Chu vi của hình hộp là diện tích của bốn hình chữ nhật bằng nhau, dài 120 cm và rộng 4 cm ::
sxq = 4.4.120 = 1920 cm2
Ví dụ 2: Mô hình một lọ thí nghiệm hình trụ (không có nắp) có bán kính hình tròn đáy là 14cm và chiều cao là 10cm. Tìm diện tích của khu vực xung quanh cộng với một cơ sở
Giải pháp:

Công thức tính diện tích toàn phần
– Giới thiệu
Tổng diện tích được tính bằng kích thước của toàn bộ không gian hình dạng bị chiếm dụng, bao gồm diện tích chu vi và diện tích của hai cơ sở được làm tròn.
-Formula
Công thức tính diện tích 2 hình tròn cơ sở
s2đ = 2πr2 (sđ = πr2)
Công thức tính diện tích toàn phần bằng diện tích xung quanh cộng với diện tích 2 đáy.
stp = sxq + 2.slow = 2.π.r2 + 2.π.r.h

Trong đó:
– r: Bán kính của hình trụ.
-h: Chiều cao của hình trụ.
– = 3,14159265359

– Ví dụ
Một hình trụ có bán kính đáy r = 4 cm và chiều cao h = 6 cm. Tính diện tích toàn phần của hình trụ đứng.
Mô tả lời giải : stp = sxq + 2.sbottom = 2.π.r2 + 2.π.r.h = 2.π.42 + 2.π.4.6 = 32π + 48π = 80π (cm2).
Ví dụ về cách tính diện tích hình trụ:
Đối với hình trụ có bán kính đáy là 6 cm , chiều cao nối đáy và đỉnh của hình trụ dày 8 cm. Chu vi và diện tích toàn phần của hình trụ là bao nhiêu?

Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:
– Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
-Tổng diện tích của hình trụ = 2 Π x r x (r + h) = 2 x π x 6 x (6 + 8) = ~ 527 cm2.
Ví dụ
Ví dụ 1: Tính diện tích toàn phần của một hình trụ có đường tròn đáy là 10cm và khoảng cách giữa hai đáy là 6cm.

Giải
Theo đề bài: h = 6cm; 2r = 10cm => r = 5cm.
Áp dụng công thức để tính diện tích toàn phần của hình trụ:
stp = 2πr (r + h) = 2π.5 (5 + 6) = 110π (cm2)
=> Vậy diện tích toàn phần của hình trụ là 110π (cm2)
Ví dụ 2: Tính diện tích toàn phần của hình trụ có chiều cao 7cm và diện tích xung quanh là 310 (cm2)

Giải
Theo chủ đề của chúng tôi: h = 7; sxq = 310
Áp dụng công thức để tính diện tích xung quanh sxq = 2πrh
= & gt; r = sxq2πrh = 3102π.7≈7cm
Vậy sđ = πr2 = π.72 = 49π≈154cm2
=> Diện tích toàn phần của hình trụ: stp = 2.sđ + sxq = 2.154 + 310 = 618cm2
Công thức tính thể tích xi lanh
– Giới thiệu
Thể tích của một hình trụ là khoảng không gian mà nó chiếm.
-Formula
Công thức cho thể tích của một hình trụ bằng diện tích của đáy nhân với chiều cao.
v = .r2.h.
Ở đâu :
– r: Bán kính của hình trụ.
-h: Chiều cao từ đáy đến đỉnh của hình trụ.
– = 3,14159265359

– Ví dụ
Một hình trụ có bán kính đáy r = 8 cm và chiều cao h = 6 cm. Tính chu vi, diện tích toàn phần và thể tích của hình trụ.
Mô tả lời giải : Thể tích của khối trụ: v = π.r2.h = π.64,6 = 384π (cm3).
– Ví dụ về cách tính diện tích của hình trụ:
Đối với bất kỳ hình lăng trụ nào có bán kính đáy là r = 4 cm , chiều dài đường nối chiều cao từ đỉnh của hình trụ đến đáy của hình trụ là h = 8 cm . >. Hình trụ này có thể tích là bao nhiêu?

Theo đó, ta áp dụng vào công thức tính thể tích hình trụ và có: bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
v = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Ví dụ 2: Một hình trụ có chu vi đáy là 20 cm và diện tích xung quanh là 14 cm². Tính chiều cao của khối trụ và thể tích của khối trụ.
Giải pháp:
Diện tích hình trụ: sxq = đáy x cao = 2 x π x r x h = 20 x h = 14
→ h = 0,7 (cm)
Chu vi đáy là 20cm → 2 x π x r = 20 → r ~ 3,18 cm
Thể tích xi lanh: v = π x r2 x h ~ 219,91 cm3
Ví dụ 3: Một hình trụ có tổng diện tích gấp đôi diện tích xung quanh, bán kính đáy là 6cm. Tính thể tích của khối trụ.
Giải pháp:
Tổng diện tích gấp đôi diện tích xung quanh: stp = 2sxq
→ 2 x 2 x π x r x h = 2 x π x r x (r + h) → 2h = 6 + h → h = 6 (cm)
Thể tích xi lanh: v = π x r2 x h ~ 678,58 cm3
Hình trụ là gì?
Hình trụ là hình được bao bởi hai hình tròn có đường kính bằng nhau và một hình trụ.

Hình trụ tròn là hình trụ khi quay hình chữ nhật quanh trục cố định, 2 đáy là hình tròn bằng nhau và song song với nhau.
Xi lanh là hình trụ có các đáy bằng nhau và song song. Hình trụ rất phổ biến trong các bài toán hình học từ cơ bản đến phức tạp, trong đó các công thức tính diện tích và thể tích của hình trụ thường được sử dụng theo nhiều cách khác nhau. Nếu bạn đã biết cách tính diện tích và chu vi hình tròn, bạn có thể dễ dàng suy ra các công thức về thể tích, chu vi và diện tích toàn phần của hình trụ.
Nhà xuất bản: thpt Sóc Trăng
Danh mục: Giáo dục