Chuyên về số thập phân hữu hạn. Lặp lại các số thập phân vô hạn
Một số thập phân hữu hạn là gì? Số thập phân vô hạn tuần hoàn là gì? Dạng toán cơ bản của số thập phân hữu hạn và số thập phân vô hạn tuần hoàn là gì? Những câu hỏi này sẽ được thpt moon giải đáp trong bài viết tiếp theo. Nếu bạn còn chưa đồng ý về kiến thức Đại số 7 này, hãy chia sẻ nhé!
Tôi. Lý thuyết chung về số thập phân
Học sinh học lý thuyết chung về số thập phân trong Toán 5 và Toán 7, đồng thời học đại số nâng cao hơn: Hiểu về số thập phân hữu hạn, số thập phân lặp lại vô hạn. Nhưng trước khi bắt đầu, chúng ta hãy xem lại lý thuyết chung về số thập phân!
Bạn đang xem: số thập phân hữu hạn. Lặp lại các số thập phân vô hạn
1. Khái niệm:
Các số: 1,8; 6,26; 0,534 được gọi là số thập phân.
2. Số thập phân vô hạn tuần hoàn là gì?
Khái niệm: Nếu một phân số đơn giản có các ước nguyên tố khác 2 và 5 ở mẫu số của nó, thì phân số đó có thể được viết dưới dạng số thập phân vô hạn tuần hoàn có lặp lại. p>
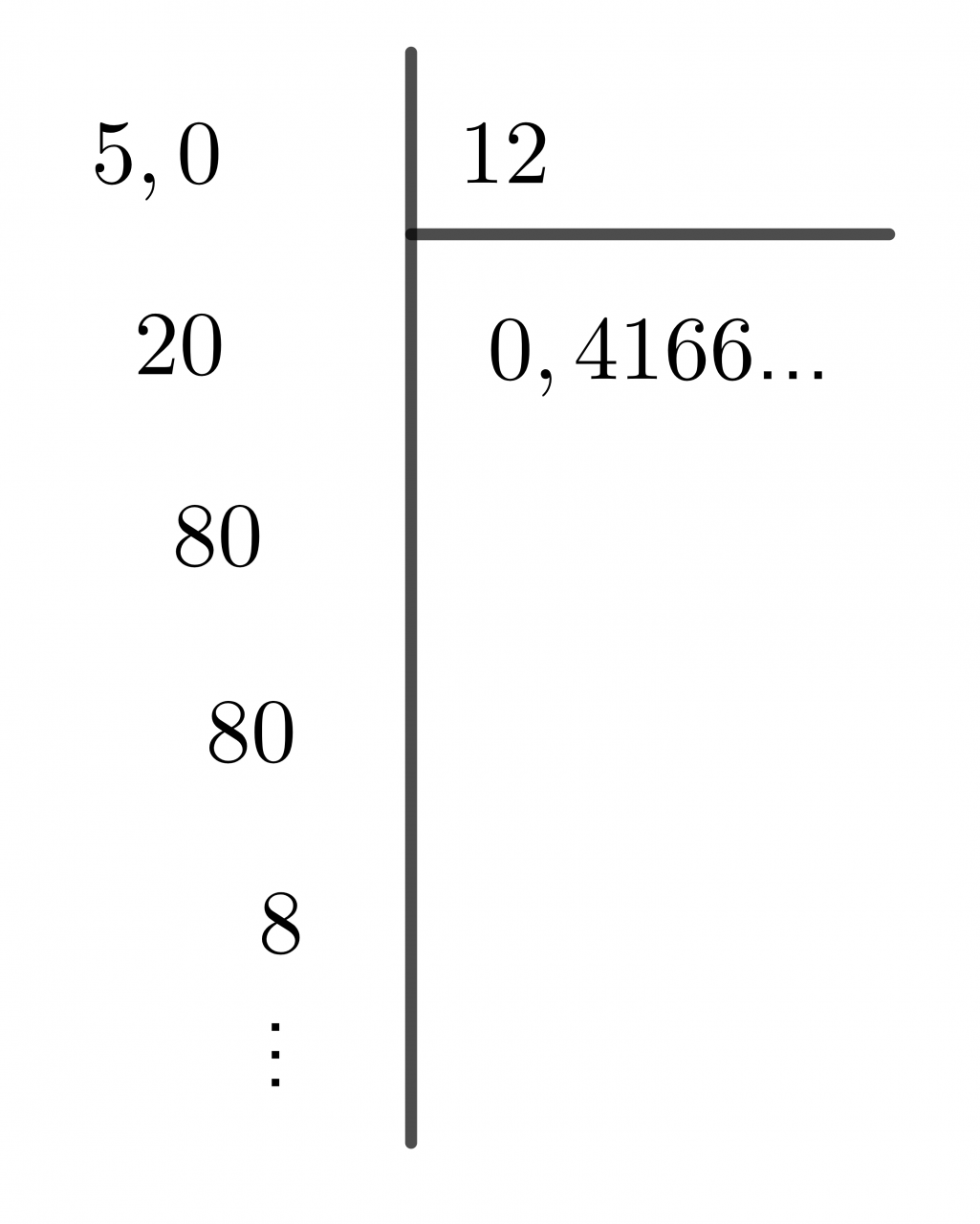
Ví dụ: Viết số 5/12 dưới dạng số thập phân.
Chúng ta làm điều tương tự với quy tắc chia hai số tự nhiên:

Rõ ràng, sự phân chia trên sẽ không bao giờ kết thúc. Nếu chúng ta tiếp tục chia, số 6 trong thương sẽ lặp đi lặp lại. Ta nói: khi chia 5 cho 12, ta được 0,4166….
Chúng tôi gọi 0,4166 … số thập phân vô hạn lặp lại , có thể được rút ngắn thành 0,14 (6)
Ba. Dạng toán số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
Dạng 1: Viết tỉ số hoặc phân số thành số thập phân
Giải pháp:
Để viết tỉ số hoặc phân số a / b dưới dạng số thập phân, ta chia a: b.
Ví dụ:
Trả lời
Dạng 2: Viết số thập phân hữu hạn dưới dạng phân số
Giải pháp:
- Viết phân số hữu hạn dưới dạng phân số mà tử số là số nguyên gồm phần nguyên và phần thân của số đó, mẫu số là lũy thừa của 10 và số mũ bằng phân số của các chữ số ở phần phân số;
- Đơn giản các phân số trên.
Ví dụ:
Viết số thập phân hữu hạn dưới dạng phân số
a, 0,32
b, -0.124
c, 1,28
d, -3,12
Giải pháp:

Dạng 3: Viết số thập phân vô hạn lặp lại dưới dạng phân số đơn giản
Giải pháp.
Để giải được bài toán này, bạn cần có thêm kiến thức về:
- Việc lặp lại các số thập phân vô hạn được gọi là đơn giản nếu vòng lặp bắt đầu ngay sau dấu phẩy, chẳng hạn như 0, (31); nếu dấu chấm không bắt đầu ngày sau dấu phẩy, nó được gọi là hỗn hợp, chẳng hạn như 0,3 ( 13). Phần phân số trước kỳ được gọi là phần không đều.
- Các giai đoạn sau đã được chứng minh:
a) Để viết phần phân số của một số thập phân vô hạn lặp lại đơn giản dưới dạng phân số, chúng tôi sử dụng dấu chấm làm tử số và mẫu số là một số bao gồm số 9, bằng số chữ số trong khoảng thời gian.
b) Để viết phần thập phân của số thập phân vô hạn tuần hoàn dưới dạng phân số, chúng ta lấy số có chứa phần bất thường và dấu chấm trừ phần bất thường làm tử số và mẫu số là số gồm 9 và 0 Số 9 bằng số chữ số của chu kì, số 0 bằng số chữ số của phần không vĩnh viễn.

Dạng 4: Nhận ra một số có thể viết dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn
Giải pháp:
- Viết phân số dưới dạng phân số có mẫu số dương.
- Giải các mẫu số dương thành thừa số nguyên tố.
- Phép nhân: Nếu không có thừa số nguyên tố, phân số có thể được viết dưới dạng số thập phân hữu hạn nếu mẫu số khác 2 và 5; nếu mẫu có các ước số nguyên tố khác 2 và 5, phân số có thể được viết dưới dạng số thập phân vô hạn tuần hoàn.
Ví dụ:
Phân số nào sau đây có thể viết dưới dạng số thập phân hữu hạn và phân số nào có thể viết dưới dạng số thập phân vô hạn lặp lại? Viết phân số dưới dạng số thập phân.
Trả lời.

Bốn. Thực hành số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
Bài 1:
Câu đố. Các số sau có bằng nhau không? 0, (31); 0,3 (13).
Giải pháp:
Chúng ta có 0, (31) – 0,3 (13) = 0,313131 … – 0,31313 … = 0
Vậy 0, (31) = 0,3 (13)
Bài 2:
Viết điểm số
Dưới dạng số thập phân.
Giải pháp:
Bài 3:
Sử dụng dấu ngoặc đơn để chỉ định các dấu chấm trong thương số (được viết dưới dạng số thập phân vô hạn lặp lại) của các phép chia sau:
a) 8,5: 3; b) 18,7: 6
c) 58: 11; d) 14,2: 3,33
Giải pháp:
a) 8,5: 3 = 2,8 (3)
b) 18,7: 6 = 3,11 (6)
c) 58: 11 = 5, (27)
d) 14,2: 3,33 = 4, (246)
Bài 4:
a) Phân số nào sau đây có thể viết dưới dạng số thập phân hữu hạn và phân số nào có thể viết dưới dạng số thập phân vô hạn tuần hoàn có lặp lại? giải thích.
b) Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn lặp lại (dấu chấm trong ngoặc ngắn)
Giải pháp:
Phân số được viết dưới dạng phân số ở dạng nhỏ nhất
– Chúng tôi có một mẫu của các phân số ở trên, không chứa các thừa số nguyên tố ngoài 2 và 5, tức là các phân số như 8, 20, 5, v.v.
Có thể được viết dưới dạng số thập phân hữu hạn.
Kết quả là
– Các phân số còn lại có thể viết dưới dạng số thập phân lặp lại.
Kết quả là
Bài 5:
Tìm một số nguyên tố duy nhất x có thể viết dưới dạng số thập phân hữu hạn. Bạn có thể điền bao nhiêu số?
Giải pháp:
Một số nguyên tố là 2, 3, 5, 7
Điền vào ô mà chúng tôi nhận được
Viết dưới dạng số thập phân hữu hạn ở trên các phân số là
Sau đó, bạn có thể điền vào 2, 3, 5
Bài 6:
Phân số nào sau đây có thể viết dưới dạng số thập phân hữu hạn và phân số nào có thể viết dưới dạng số thập phân vô hạn lặp lại? Viết phân số dưới dạng số thập phân.
Giải pháp
Ta có: Xét mẫu số của một phân số đã cho
4 = 22; 6 = 2,3; 50 = 52,2; 125 = 53; 45 = 32,5; 14 = 2,7
– Các phân số có thể viết dưới dạng số thập phân hữu hạn là:
Vì mẫu của họ không có thừa số nguyên tố nào ngoài 2 và 5
– Các phân số có thể được viết dưới dạng số thập phân vô hạn là:
Vì mẫu của chúng có các ước số chính khác 2 và 5
Bài 7:
Giải thích tại sao các phân số sau đây có thể được viết dưới dạng số thập phân lặp lại và sau đó viết chúng theo cách đó
Giải pháp:
Các phân số đã cho có mẫu số dương và tất cả các phân số đều chứa các thừa số nguyên tố khác 2 và 5, vì vậy chúng được viết dưới dạng số thập phân vô hạn lặp lại.
Chúng tôi nhận được:

Bài 8: Tìm số hữu tỉ a của x <a <Đúng, biết:
a) x = 213,6784; y = 214,5769 ….
b) x = -25,4832…; y = – 24,9736…
Giải pháp:
a) Nếu a = 213,68 hoặc a = 214,56;
b) Ví dụ a = -25,47 hoặc a = -24,98.
Bài 9: Khi viết phân số vô hạn tuần hoàn 0,481818181… dưới dạng phân số đơn giản thì mẫu số lớn hơn mẫu số:
Một, 13
b, 14
c, 29
d, 57
e, 126
Vui lòng chọn câu trả lời đúng.
Giải pháp:
Câu trả lời đúng là d.57.
Giải thích:
Chắc chắn là: 110 – 53 = 57.
Bài tập 10: Tìm x, biết: 0, (26) .x = 1,2 (31)
Vì vậy, thpt sóc trăng đã chia sr hoàn toàn để tập trung vào số thập phân hữu hạn. Số thập phân lặp lại vô hạn. Hy vọng rằng bạn đã nắm được phần quan trọng nhất của kiến thức toán học của bạn. Quyền hạn của số hữu tỉ cũng được đề cập chi tiết. Đừng bỏ lỡ!
Nhà xuất bản: thpt Sóc Trăng
Danh mục: Giáo dục