Trong toán học hình học không gian, lăng trụ là một trong những hình dạng của không gian. Nó có nhiều dạng khác nhau, chẳng hạn như lăng trụ đứng, lăng trụ tam giác đều và lăng trụ tứ giác đều, với các tính chất và công thức khác nhau. Bài viết dưới đây sẽ giúp các em nắm vững một trong các dạng hình lăng trụ thường gặp là hình lăng trụ tam giác đều với các dạng bài tập từ cơ bản đến nâng cao để các em có thể vận dụng. Sử dụng sau lớp học.
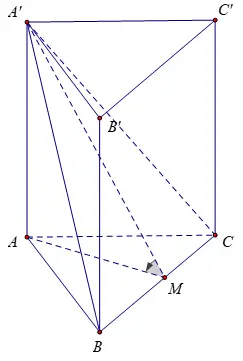
Hình lăng trụ là một hình đa diện gồm hai đáy là hai đa giác bằng nhau và nằm trong hai mặt phẳng song song, có các cạnh bên là hình bình hành có các cạnh đối song song hoặc bằng nhau
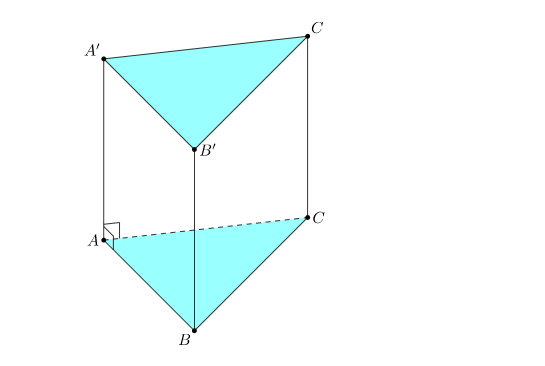
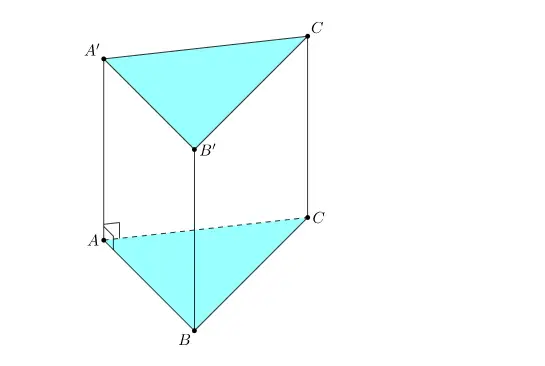
Hình lăng trụ tam giác đều là hình lăng trụ có đáy là hai tam giác đều.
lăng trụ tam giác đều
Tính chất của lăng trụ tam giác đều
Tính chất của hình lăng trụ tam giác đều:
- Hai đáy là hai tam giác đều nên hai đáy là đồng dư.
- Các cạnh bên vuông góc với đáy.
- Một bên là một bên. hình chữ nhật.
Công thức thể tích của lăng trụ tam giác đều
Thể tích của hình lăng trụ bằng khoảng cách hoặc chiều cao giữa diện tích đáy và hai đáy. Công thức thể tích khối lăng trụ tam giác đều
v = b.h
Trong đó: b là diện tích của đáy, h là chiều cao của lăng trụ và v là thể tích của lăng trụ
Mặt đáy của lăng trụ tam giác đều là tam giác đều. Gọi a là diện tích tam giác đều, ta có công thức tính diện tích tam giác đều sau:
Bài tập 1
Tính thể tích của khối trụ tam giác đều abca’b’c ‘có độ dài đáy là 8cm và mặt phẳng a’b’c’ tạo với đáy abc một góc 60o.
Trả lời:
Gọi tôi là trung điểm của đoạn thẳng bc mà chúng ta có:
ai vuông góc với bc (theo tính chất đường trung tuyến của tam giác đều)
a’i vuông góc với bc (vì a’bc là tam giác cân)
- Góc a’bc, abc = góc aia ‘= 600
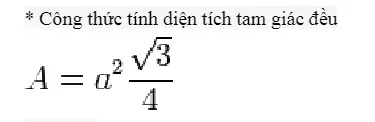
Diện tích tam giác abc:
- Thể tích của khối lăng trụ tam giác đều abca’b’c ‘là:
Bài tập 2
Tính thể tích của khối lăng trụ tam giác đều abca’b’c ‘, có đáy là tam giác nội tiếp đường tròn bán kính a và diện tích mặt bên của lăng trụ là
Bài tập 3
Chiều cao của hình lăng trụ tam giác đều abca’b’c ‘là a. Tính thể tích khối lăng trụ cho mặt phẳng có góc đáy là 300 (abc ‘)
Bài tập 4
Một hình lăng trụ tam giác đều abca’b’c ‘có đáy là a. Diện tích tam giác abc ‘là
Tính thể tích của lăng trụ
Bài tập 5
Một lăng trụ tam giác abca’b’c ‘có đáy abc là tam giác đều cạnh a. Đỉnh a ‘của lăng trụ cách đều a, b và c. Mặt aa ‘hợp với mặt đáy một góc 600. Tính thể tích của khối lăng trụ.
Bài tập 6
Cho lăng trụ tam giác đều abca’b’c ‘có đáy là a, chiều cao gấp đôi đáy. Gọi e, f lần lượt là trung điểm của các cạnh aa ‘, bb’. Tính tỉ số thể tích của hình nón c.abef với thể tích của hình lăng trụ đã cho
Bài tập 7
Cho hình lăng trụ đứng, tất cả các cạnh của tam giác abca’b’c ‘đều bằng a. Tính thể tích của khối tứ diện a’bb’c.
Bài tập 8
Đối với hình lăng trụ đứng, đáy của tam giác abca’b’c ‘là tam giác vuông, tại a, ac = b và góc acb bằng 600. Góc tạo bởi đường thẳng bc ‘và mặt phẳng aa’c’c là 300.
Tính độ dài của đoạn thẳng ac ‘
Tính thể tích của một lăng trụ đã cho
Bài tập 9
Cho khối lăng trụ tam giác abca’b’c ‘, đáy của nó là tam giác đều cạnh a, điểm a’ cách đều 3 điểm a, b, c và cạnh aa ‘cách mặt đáy 600 độ. góc mặt phẳng.
Tính thể tích của khối lăng trụ đó
Chứng minh rằng cạnh bcc’b ‘là hình chữ nhật
Tính tổng diện tích mỗi mặt của hình lăng trụ tam giác abca’b’c ‘
Bài tập 10
là hình lăng trụ tam giác đều abca’b’c ‘. Gọi m là trung điểm của cạnh aa ‘. Chia hình lăng trụ thành hai phần bởi các mặt phẳng của m, b ‘, c. Tính tỉ số thể tích của hai phần.
Bài tập 11
Cho lăng trụ tam giác đều chiều cao h, bao quanh một mặt cầu bán kính r (h <2r) (lăng trụ tam giác đều nội tiếp một mặt cầu nên sáu đỉnh của lăng trụ sẽ nằm trên mặt cầu).
p>
a) Tính đáy của lăng trụ.
b) Tính thể tích của khối lăng trụ.
c) Tính h từ r để mỗi mặt của lăng trụ là một hình vuông.
Trả lời:
a) Gọi o là tâm đường tròn ngoại tiếp lăng trụ và i là hình chiếu của o trên mặt phẳng (abc). Sau đó, chúng tôi có:
oa = ob = oc = r
oi = 1 / 2.h
Tam giác ai là tam giác vuông tại i nên ai2 – oi2 = r2 – 1 / 4.h2
ia là bán kính của đường tròn ngoại tiếp tam giác đều abc, do đó
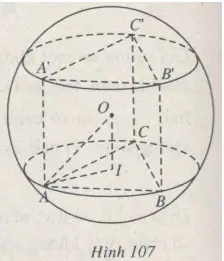
Vì vậy, các đáy của các lăng trụ đều bằng nhau
b) Thể tích của khối lăng trụ abc.a’b’c ‘là
c) Mỗi mặt của lăng trụ là một hình vuông nếu và chỉ khi ab = h, tức là
Bài tập 12
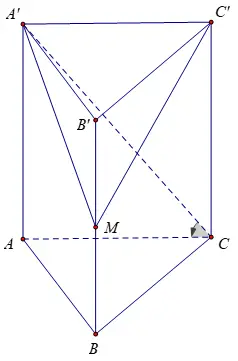
Cho lăng trụ đứng abc.a’b’c ‘là tam giác đều có đáy a√3, góc giữa và góc đáy bằng 60º. Gọi m là trung điểm của. Tìm thể tích của hình chóp m.a’b’c ‘
Trả lời:
do aa ‘vuông góc với tam giác abc, do đó nó được suy ra
(a’c, (abc)) = góc a’ca = 60º
Chúng ta có aa ‘= ac. tan
= a√3.tan60º = 3a
Bài tập 13
Cho lăng trụ đứng abc.a1 b1 c1 có đáy abc là tam giác vuông cân tại b, trong đó ba = bc = 2a, cho trước a1 m = 3a, với m là trung điểm của bc. Tính thể tích khối lăng trụ abc.a1 b1 c1
Trả lời:
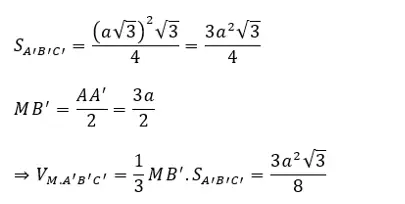
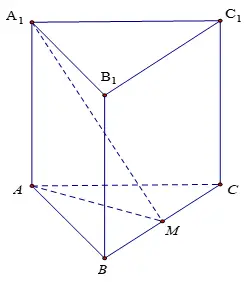
Bài tập 14
Cho lăng trụ đứng có đáy abc.a’b’c ‘trong đó ab = a; ac = 2a và ∠ (bac) = 120º, mặt phẳng (a’bc) cách đáy 60º. Tính thể tích của khối lăng trụ abc.a’b’c ‘
Trả lời:
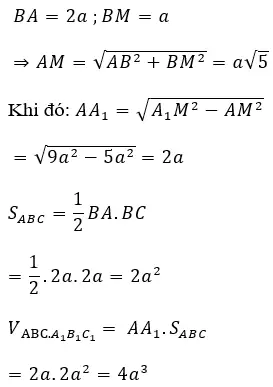
Dựng một đường vuông góc với bc mà chúng ta nhận được
a’m vuông góc với bc, aa ‘vuông góc với bc => (aa’m) vuông góc với bc
= & gt; vuông góc với bc
Tam giác a’bc cắt tam giác abc = bc