Hướng dẫn hồi quy xác suất trên phần mềm stata, hướng dẫn chạy lệnh phần mềm stata để chạy hồi quy xác suất, đọc kết quả hồi quy, các bài kiểm tra cần thiết để chạy mô hình này, hướng dẫn cách dễ dàng hiểu hồi quy xác suất nhị phân với hai giá trị xác suất …
Hiểu các mô hình xác suất
Hồi quy xác suất, còn được gọi là mô hình xác suất, được sử dụng để lập mô hình các biến kết quả nhị phân hoặc nhị phân. Trong mô hình probit, nghịch đảo của phân phối chuẩn xác suất được mô hình hóa như một sự kết hợp tuyến tính của các yếu tố dự đoán.
Xin lưu ý: Mục đích của trang này là hiển thị cách sử dụng các lệnh phân tích dữ liệu khác nhau. Nó không bao gồm tất cả các khía cạnh của quá trình nghiên cứu mà một nhà nghiên cứu nên thực hiện. Đặc biệt, nó không bao gồm việc làm sạch và kiểm tra dữ liệu, xác thực giả thuyết, chẩn đoán mô hình và phân tích theo dõi tiềm năng.
Mô hình xác suất là các thông số kỹ thuật chung cho các mô hình phản hồi nhị phân hoặc nhị phân. Vì vậy, nó sử dụng các kỹ thuật tương tự để giải quyết cùng một tập hợp các vấn đề như hồi quy logistic. Mô hình xác suất sử dụng các hàm tương quan xác suất thường được ước tính bằng cách sử dụng quy trình khả năng xảy ra tối đa tiêu chuẩn, một ước lượng được gọi là hồi quy xác suất .
Ứng dụng hồi quy mô hình probit
Để bắt đầu tìm hiểu về hồi quy xác suất, chúng tôi sử dụng các tập dữ liệu sau:
Vị trí:
- admin: biết rằng nhị phân cũng là một biến phụ thuộc
- gre, gpa là một biến liên tục
- xếp hạng là một biến phân cấp
Trước khi quay lại, chúng ta cần ôn lại một số kiến thức như sau:
Sau đây là danh sách một số phương pháp phân tích mà bạn có thể gặp phải. Một số phương pháp được liệt kê là khá hợp lý, trong khi những phương pháp khác không phổ biến hoặc hạn chế.
Hồi quy xác suất, trọng tâm của bài viết này
Hồi quy logistic. Mô hình logit sẽ tạo ra kết quả tương tự như hồi quy theo xác suất. Sự lựa chọn giữa probit và logit phần lớn là vấn đề sở thích cá nhân.
Quay lại ols. Khi được sử dụng với các biến phản hồi nhị phân, mô hình được gọi là mô hình xác suất tuyến tính và có thể được sử dụng như một cách để mô tả các xác suất có điều kiện. Tuy nhiên, các lỗi (tức là phần dư) của mô hình xác suất tuyến tính vi phạm giả định sai số hồi quy về tính đồng nhất và tính chuẩn, dẫn đến sai số chuẩn và tỷ lệ kiểm định giả thuyết rỗng.
Để có thảo luận sâu hơn về những vấn đề này và các vấn đề khác với mô hình xác suất tuyến tính, hãy xem long (1997, trang 38-40).
Phân tích chức năng phân biệt hai nhóm này. Các phương pháp đa biến cho các biến kết quả nhị phân. Khách sạn 2. Kết quả 0/1 được chuyển thành nhóm biến và dự đoán trước đó được chuyển thành kết quả biến. Điều này sẽ mang lại một bài kiểm tra tổng thể có ý nghĩa, nhưng sẽ không cung cấp các hệ số riêng lẻ cho từng biến và sẽ không rõ mỗi “dự đoán” đã được điều chỉnh ở mức độ nào đối với ảnh hưởng của biến kia. đoán. “
Hồi quy xác suất
Đối với hồi quy xác suất, chúng tôi sử dụng lệnh sau:
probit công nhận xếp hạng của gre gpa
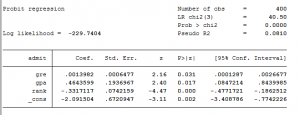
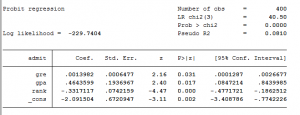
Giá trị p của chúng tôi là & lt; 5%, do đó, mô hình có ý nghĩa thống kê.
Đồng thời, giá trị p của ba biến phụ thuộc gre, gpa và rank đều <5%, vì vậy ba biến này có ý nghĩa thống kê.
Khi gre tăng 1 đơn vị, điểm z tăng 0,001 đơn vị
Z-core tăng 0,464 đơn vị khi gpa tăng 1 đơn vị
Thứ hạng biến là một biến thứ hạng, vì vậy mỗi khi thứ hạng tăng lên 1 bậc, điểm z sẽ giảm đi -2,01. Điều này có nghĩa là số bước được thêm vào hoặc bị trừ đi trong mô hình là như nhau, điều này không chính xác. Chúng ta cần phải tìm ra ảnh hưởng của thứ hạng = 3 đối với sự công nhận là lớn như thế nào?
Xác suất thừa nhận gre gpa i.rank
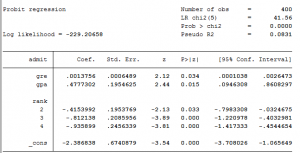
Tham gia với một đơn vị ở hạng = 2 sẽ dẫn đến giảm 0,4 đơn vị điểm z so với một đơn vị ở hạng = 1.
Nhân tiện, chúng tôi kiểm tra rằng biến phụ thuộc của thứ hạng không bằng = 0 tại cùng một thời điểm
Kiểm tra 2.rank 3.rank 4.rank

kiểm tra cho thấy rằng các biến độc lập i.rank không phụ thuộc vào nhau và ảnh hưởng có ảnh hưởng độc lập đến việc nhập học.
Tìm độ nhạy biên của mô hình
Chúng tôi nhận thấy mức độ nhạy cảm của các biến xếp hạng đối với các biến kết nạp
Xếp hạng ký quỹ, Trung bình
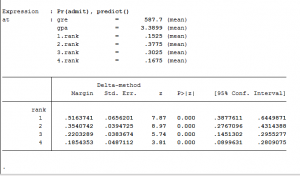
Sau khi chúng tôi chạy margin, chúng tôi nhận được các kết quả sau:
Có 0,52 (52%) xác suất để chúng ta có một thứ hạng = 1 và 19% xác suất xếp hạng = 4.
Kiểm tra thống kê fitstat
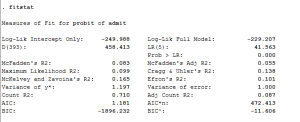
Trong hồi quy mô hình xác suất, chúng ta nên kiểm tra sự phù hợp thống kê.
Những điều cần xem xét
Các ô trống hoặc ô nhỏ: Bạn nên kiểm tra các ô trống hoặc ô nhỏ bằng cách gạch chéo giữa các biến dự đoán phân loại và biến kết quả. Nếu có một vài trường hợp của một ô (một ô nhỏ), mô hình có thể trở nên không ổn định hoặc hoàn toàn không chạy.
Phân tách hoặc phân tách (hay còn gọi là dự đoán hoàn hảo), tức là điều kiện mà kết quả không thay đổi ở một mức độ nào đó của biến độc lập. Xem Câu hỏi thường gặp về trang của chúng tôi: Sự tách biệt hoàn toàn hoặc gần như hoàn toàn trong hồi quy logistic / xác suất và chúng ta giải quyết chúng như thế nào? Thông tin về các mô hình với dự đoán hoàn hảo.
Kích thước mẫu: Cả mô hình probit và logit đều yêu cầu nhiều trường hợp hơn so với hồi quy ols vì chúng sử dụng các kỹ thuật ước tính khả năng xảy ra tối đa. Hồi quy logistic chính xác (sử dụng lệnh exlogistic) đôi khi có thể được sử dụng để ước tính mô hình kết quả nhị phân trong bộ dữ liệu chỉ với một số trường hợp. Để biết thêm thông tin, hãy xem Ví dụ về Phân tích Dữ liệu của chúng tôi cho Hồi quy Logistic Chính xác. Cũng cần lưu ý rằng khi kết quả rất hiếm, có thể khó ước tính một mô hình xác suất ngay cả khi tổng lượng dữ liệu lớn.
Pseudo r-squared: Có nhiều thước đo bình phương giả r khác nhau. Cả hai đều cố gắng cung cấp thông tin tương tự như thông tin được cung cấp bởi r bình phương trong hồi quy ols; tuy nhiên, cả hai đều không thể được hiểu đầy đủ là bình phương r trong hồi quy ols được diễn giải. Để biết thảo luận về r bình phương giả khác nhau, hãy xem dài và tự do (2006) hoặc trang Câu hỏi thường gặp của chúng tôi R-bình phương là gì?
Trong dữ liệu, giá trị 0 là cấp đầu tiên của biến kết quả và tất cả các giá trị không bị thiếu khác là cấp thứ hai của biến kết quả.
Chẩn đoán: Chẩn đoán hồi quy probit khác với chẩn đoán hồi quy ols. Chẩn đoán của mô hình probit tương tự như chẩn đoán của mô hình logit. Để biết thảo luận về chẩn đoán mô hình hồi quy logistic, hãy xem hosmer và lemeshow (2000, Chương 5).
Hướng dẫn hồi quy logit trên spss
Hướng dẫn hồi quy xác suất về dữ liệu
Giới thiệu về hướng dẫn hồi quy tobit của stata